Now that we have seen that image distance and object distance are closely tied to each other and the focal length, we can get into how these distances apply to real life. The image distance and the focal length are mathamatically related to the image magnification and working distance at the magnification. First a few words about magnification to make things more clear.
Magnification, as it applies to photography, is the ratio of the detector size divided to the size of the object that fits on the detector. If I can fit a 30 mm coin onto a 15 mm detector the magnification is 15/30 which translates into 1:2 or 0.5x - the image is half life size. If I fit a 7.5 mm coin onto a 15 mm detector, the magnification will be 2:1 or 2x - the image is twice life size. The example below shows that the field is about 9.6 mm wide. My detector is 23.6 mm wide. That corresponds to a magnification of about 2.5:1.

As stated previously, there is a mathamatical association between the image distance and the magnification.
i = f(m+1)(where i=image distance, f=focal length, m=magnification)

There are a few interesting associations that come out of this equation. First, at a magnification of zero (infinity focus). i equals the focal length of the lens (this point came up in the previous posting). As stated previously, the detector must be one focal length behind the lens to focus at infinity. Second, if you add one more focal length of image distance (also called extension), you will now be focusing at 1:1 - life size on the detector. A 100 mm lens will require an extra 100 mm of extension to focus at 1:1 compared to infinity focus. For every extra 1x of magnification beyond 1:1 you will need to add one focal length of extension. Longer focal length lenses require proportionally more extension to get to the same magnification as shorter focal length lenses.
Object distance (roughly the working distance)is inversely proportional to the magnification.
o = f((1/m) + 1) (where o=object distance, f=focal length, m=magnification)
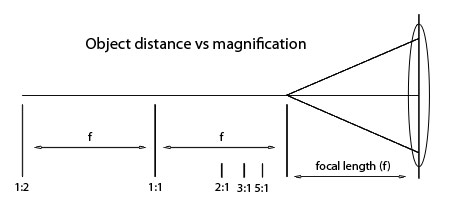
As with the previous equation there are a couple of interesting associations to come out. As the magnification get higher, 1/m approaches zero and the working distance approaches the front focal length of the lens. At 1:1 magnification the object distance will be 2f (the same as the image distance).
All high-magnification work (above 1:1) will have working distances from 1-2 focal lengths from the center of the lens while typical macro lenses that work up to 1:1 magnification will have image distances from 1-2 focal lengths of the lens.
If you add the image distance and the object distance you will get the detector to object distance that I will call the camera distance. This is the distance from your camera (detector) to the object being photographed. This number works only for simple lenses and will need to have a slight modification when used with photographic lenses (will be discussed in a later installment).
cd = f(m + (1/m) + 2) (where cd=camera distance, m=magnification, f=focal length)
The interesting association to come out of this equation is that the minimum camera distance will be achieved at 1:1 and will be 4f. At any other magnification lower and higher, the distance will be larger. A 100 mm lens will have a minimum camera distance of 400 mm at 1:1. I can anticipate getting angry comments suggesting that their camera with a 100 mm lens has a camera distance significantly less than 400 mm when focusing at 1:1. To that I will reply: most modern macro lenses shorten the focal length as the magnification is increased. You can get a rough estimate of that focal length by dividing the distance by 4.
For normal photography (less than 1:1 magnification) the camera will move toward the subject as the magnification increases. For photography above 1:1, the camera will move farther away as the magnification increases.