We have already discussed the effect of aperture on resolution. The larger the aperture, the more potential resolution in the system. The size of the aperture is not the only factor, as the distance that the aperture is from the focus plane also determines the resolution. These two factors determine the angle that the rays exiting the aperture make with the focus plane . The angle determines the amount of diffraction, and diffraction is the ultimate determinant of resolution.
If the aperture is twice as far away from the focus plane, it will have to be twice as big to make the same relative angle with the focus plane. This is where the effective aperture come into play as it accounts for the size and the distance that the aperture is from the focus plane. the effective aperture is easily calculated:
Effap = N *(m+1) (where N = aperture setting, m = magnification)
The effective aperture has a direct association with the resolution of a system. I have said this before, but wanted to make the same statement in graphical form. Below is a graph of all but one of the lenses that I have so far tested for this website. The graph shows the MTF10 (resolution) as a function of effective aperture. You will see that all the lenses but one cluster quite close to a smooth curve. As the effective aperture goes up, the resolution decreases. This decrease is a result of worsening diffraction as the effective aperture rises.
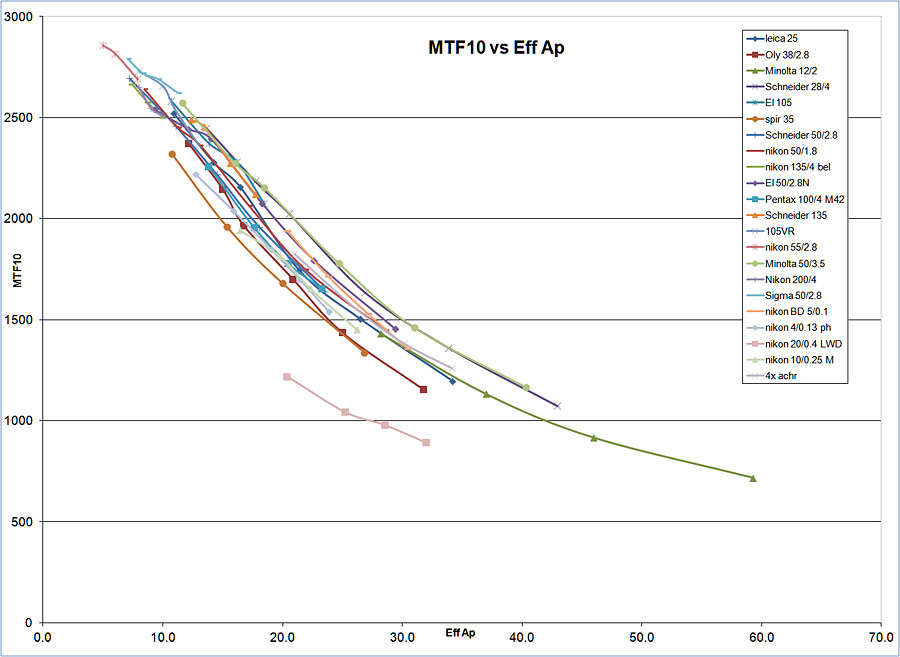
So, what does all this mean? The main point is that decreasing the effective aperture will increase the potential resolution of a system. That doesn't mean that you should just open up the aperture to its largest size (smallest number). It does mean that if you want the most resolution, you should open the lens up to its most resolving aperture. If you open the lens up further, lens aberrations will start to negatively affect the resolution. I address this issue in my lens tests.
Another point to think about is that all lenses don't have the same aperture as their most resolving aperture. One lens may be best at f/2.8 and another may be best at f/8. When working at the same magnification, the f/2.8 lens will almost invariably out-resolve the lens that works best at f/8.
What allows a lens to work better at a larger aperture? I have found two main factors: focal length and price. Focal length is the main determinant from my own testing experience. Shorter focal length lenses tend to have larger apertures as their most resolving. If you want the most resolution, choose the lens (that works well at the magnification you need) of the shortest focal length that still maintains an adequate working distance. If you need long working distance, by all means choose a longer focal length lens.
Price also effects the largest/highest resolving aperture of a lens. It just costs more to make a larger aperture lens. Microscope objectives are a good example of the cost vs performance association. APO microscope objectives are extremely expensive and with that price comes larger apertures and higher resolution capabilities.
To address the one lens that fell out of the cluster on the above graph: The Nikon 20x 0.40 LWD objective. I think that this lens suffers for a couple reasons: a very large aperture (just over f/1) and a long working distance. Price also likely plays into the equation, but I don't know what it's list price was. Making a lens with those attributes at a reasonable price requires some compromise. That being said, when this lens' resolution is graphed vs. magnification it has the highest resolving power of any lens that I have yet tested.